期中成绩出了吗?
不论成绩如何,
我们最关键的是要学会复盘!
尤其是数理化,
只有把错题都理顺了,
才能避免再次掉进同一个坑里。

锐角三角比看似简单,
却是综合性习题的基础,
特别是现实问题的建模转化,
几乎是每一张卷子都有,
所以——
快快练起来啦~

这次有答案有解析,
大家如果有新的思路,
也欢迎在评论区分享!
例题解析
基础定义理解
如图,Rt△ABC 中,∠C=90°,∠B= 30°,AD 是∠BAC 的角平分线,AC=6,则点 D到 AB 的距离为_______
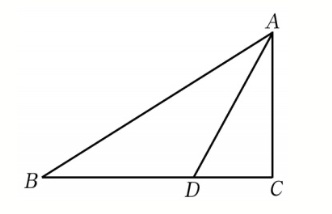
分析:
过点D作DE⊥AB于E,根据直角三角形两锐角互余的性质可得∠BAC= 60°,由AD为∠BAC的角平分线可得∠DAC=30°,根据角平分线的性质可得DE=CD,利用∠DAC的正切求出CD的值即可得答案。
解:
作 DE⊥AB 于点 E,
∵∠C=90°,∠B=30°,
∴∠BAC=60°,
∵AD 平分∠BAC,
∴∠DAC=30°,DE=CD,
∵AC=6,
∴CD=tan∠DAC =2√3,即DE=2√3,
∴点D到AB的距离为2√3.

如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6米到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°,则该电线杆PQ的高度( )米
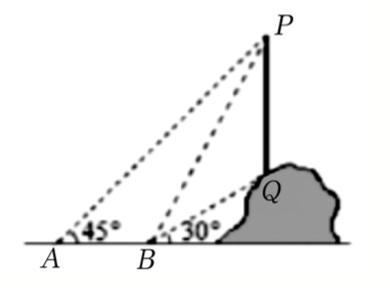
(点击选项查看答案)
小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走了1300米,此时小明看山顶的角度为60°,则山高( )米
(点击选项查看答案)
在一次数学活动,嘉淇利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD。
如图,嘉淇与假山的水平距离BD为6米,他的眼睛距地面的高度为1.6米,嘉淇的视线经过量角器零刻度线OA和假山的最高点C,此时,铅垂线OE经过量角器的60°刻度线,则假山的高度CD为( )
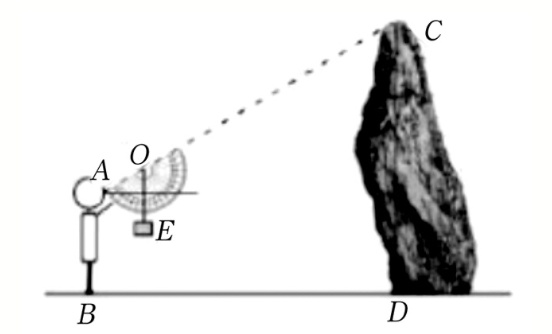
(点击选项查看答案)
如图,在一次巡航中,预警机沿AE方向飞行,驱护舰沿BP方向航行,且航向相同(AE∥BP)。当预警机飞行到A处时,测得航行到B处的驱护舰的俯角是45°,此时B距离相关岛屿P恰为60千米;当预警机飞行到C处时,驱护舰恰好航行到预警机正下方D处,此时CD=10千米;当预警机继续飞行到E处时,驱护舰到达相关岛屿P,且测得E处的预警机的仰角为22°。
求预警机的飞行距离AE。(结果保留整数)
(参考:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40)

如图,在东西方向的海岸线l上有一长为1千米的码头MN,在距码头西端M的正西方向58千米处有一观测站O。现测得位于观测站O的北偏西37°方向,且与观测站O相距60千米的小岛A处有一艘轮船开始航行驶向港口MN。经过一段时间后又测得该轮船位于观测站O的正北方向,且与观测站O相距30千米的B处。
(1)求AB两地的距离;(结果保留根号)
(2)如果该轮船不改变航向继续航行,那么轮船能否行至码头MN靠岸?请说明理由。
(参考:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如果有搞不懂的题目,或是需要的学科专题,欢迎在评论区留言哦~
本周隔空喊话bot
怎么说!
期中考试结束了,
你考得怎么样呀?
是收获稳稳的幸福,
还是汗流浃背地“寄”了?
有什么想吐槽的,
或者夸夸自己的,
Let’s talk!
小编先答:
看到网上有同学吐槽语文作文难评,数学最后来不及做,英语难得惊人,考完天都塌了。好吧,小编祝你成功!
⭐️ 欢迎大家点击初三了,你还愿意当班委吗?或扫码提问箱或在评论区留言~
-上海中考发布-
《上海中学生报·中招周刊》与上海市教育考试院合作
中考信息发布及学科复习方法指导
精准试卷解析权威中招政策及时模考信息历年数据查询
主流国际教育品质国际学校在线课程辅导学校特色介绍
CONTACTUS
Email:shzkfb@163.com
TEL:+86-021-33255783
如果您有任何问题,或合作意向请留言或给我们打电话吧:)